We did a lot of things in the previous 5 lessons:

• We observed a macro-level gas phenomenon (air duster can) and we tried to reason about the underlying micro-level events such as:
  • What is a gas made up of?
  • How do gas particles move in space?
  • How do gas particles interact with each other and the walls of the container?
• We tried to qualitatively understand how micro-level interactions among gas particles lead to an important macro-level property: pressure.
  • What is kinetic molecular theory?
  • What is an ideal gas?
• We qualitatively and quantitatively explored the relationship between three variables and gas pressure: number of particles, gas temperature, container volume.
  • How can we use computational models to study the behavior of gasses?
  • How can we conduct computational experiments to: collect data, analyze data, and develop mathematical models?
  • How do we validate our mathematical models?
  • In what ways our mathematical models help us reason about real-world phenomena that involves gas pressure?
     

In this final lesson, we will reflect on our hard work and try to put together all three mathematical models, as well as our understanding of the behavior of gas particles, to develop a coherent theory of ideal gases.

We started this unit with an exploration on how the "air duster can" works. Let's revisit the air duster can again, but this time, about another interesting aspect of air duster cans (and all other spray cans), the warnings:

 .         

Can we use the knowledge we constructed through previous 5 lessons to explain why we need these warning texts on spray cans?

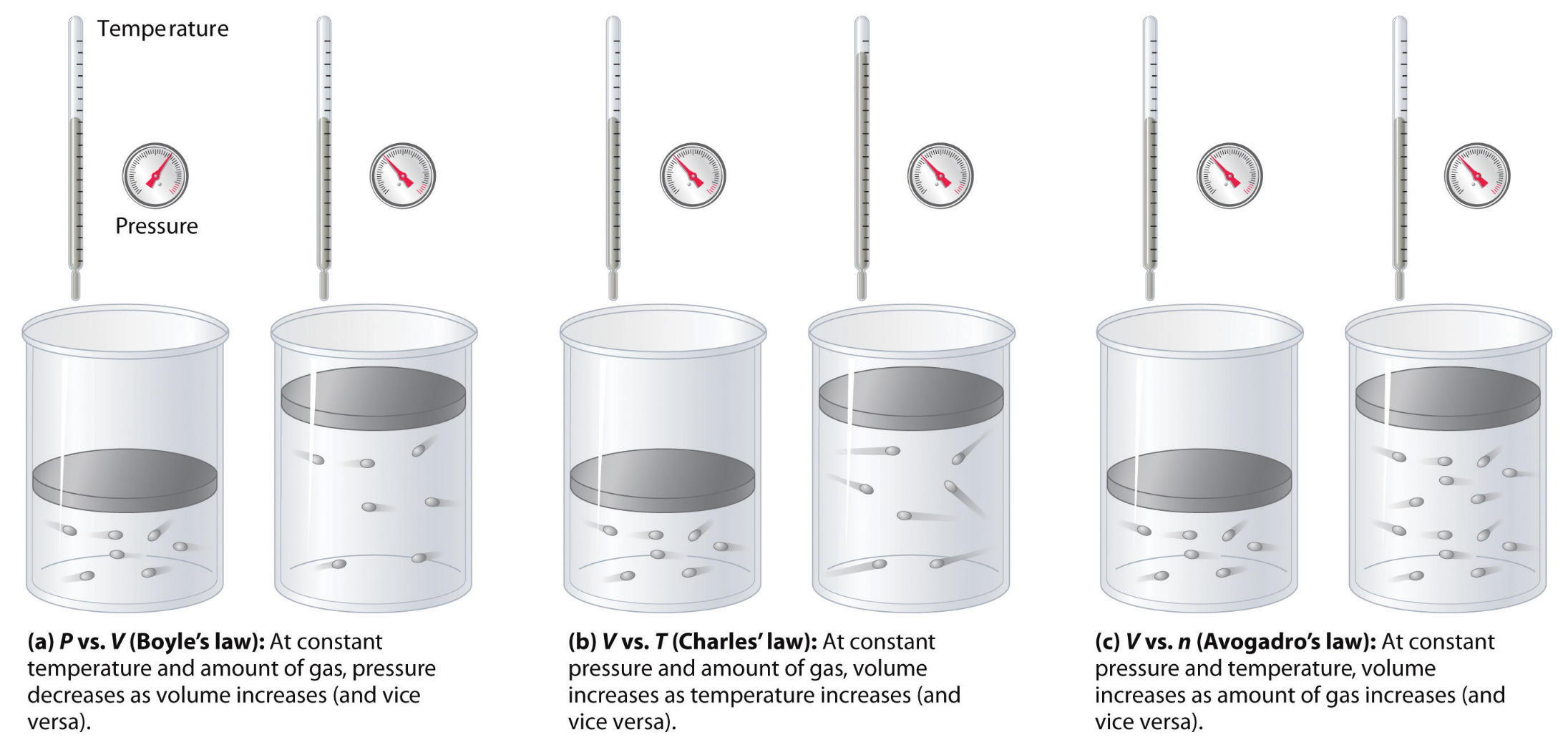
What we did in this unit was to re-develop three main gas theories using computational models and quantitative data analysis.

We defined the relationship between number of particles and pressure as:

• Qualitatively: As number of particles increases, pressure increases linearly (given that temperature and container volume are constant)
• Quantitatively: \((P)ressure = m_1 \times (N)umber \) , where \(m_1\) is a constant coefficient.

We defined the relationship between gas temperature and pressure as:

• Qualitatively: As gas temperature increases, pressure increases linearly (given that number of particles and container volume are constant)
• Quantitatively: \(P= m_2 \times (T)emperature \) , where \(m_2\) is a constant coefficient.

And, we defined the relationship between container volume and pressure as:

• Qualitatively: As gas temperature increases, pressure increases linearly (given that number of particles and container volume are constant)
• Quantitatively: \({P} = {m_3 \over (V)olume}\) , where \(m_3\) is a constant coefficient.

Our methodology and findings were analogous to three scientific discoveries made between 17^th and 19^th centuries:

However, as both the warning on the air duster can and the ballon-on-fire experiment showed, often times, we may not be able to explain gas-pressure related phenomena through just one variable. We need be combine our three theories and come up with one ideal gas theory. Let's try to do that!

Please set your computer aside briefly (do not close this page) and join the classroom discussion that your teacher is going to moderate.

Note: If your teacher did not initiate the discussion yet, you can start answering the first four questions below as you are waiting.

Let's review how we would put together our three theories mathematically:

Step 1: We would write them one by one:

\(P = m_1 \times N\)     _{(Eq. 1)}

\(P = m_2 \times T\)     _{(Eq. 2)}

\(P = {m_3 \over V}\)     _{(Eq. 3)}

Step 2: We would combine the right side of the equations:

\(P = {{(m_1 \times N) \times (m_2 \times T) \times (m_3)} \over V}\)     _{(Eq. 4)}

Step 3: We would slightly modify the equation by moving \(V\) to the other side of the equation and we would also get rid of the parentheses:

\(P \times V = {m_1 \times m_2 \times m_3 \times N \times T }\)     _{(Eq. 5)}

Finally, we would combine all three coefficients \((m_1 \times m_2 \times m_3)\)as one coefficient, which we can simply call as \(m_g\) or the ideal gas coefficient:

\(P \times V = {m_g \times N \times T }\)     _{(Eq. 6)}