Do you know what is an “air duster”? If your answer is  , explain in one sentence. If your answer is
, explain in one sentence. If your answer is  , do not just write “no”, make a guess.
, do not just write “no”, make a guess.

Unit Overview
This is a 2 week unit designed to cover high-school and introductory college level topics in the properties of gases and gas particle behavior. The unit includes eight lessons. Each lesson uses computer models to explore these topics in greater depth. The models also afford greater degree of student inquiry and guided discovery than would be typically possible through other learning activities in the same amount of time.
The computer models enable students to investigate what causes pressure in a gas, how it is measured, and how it is affected by the properties of the particles that make the gas and the characteristics of the container they are in. Students are encouraged to understand how the principles and effects of pressure are generated from specific interactions between many particles (or simplified gas molecules) and with their environment. To do this, students gain a familiarity with a microscopic view of the gas particles by running many different computer models of systems of gas particles. Some initial models are designed for orienting the student to the NetLogo interface and the practice of computer-based modeling, others are designed for specific data gathering and data analysis tasks.
The later computer models focus on how particles behave in a variety of conditions. Such conditions include varying the number of particles, the size of the particles, the speed of the particles, and the location of solid walls they bounce off. These variations support students explorations of the models to design new variations into the model (adding new rules for particle behavior, designing new system boundaries), designing experiments and testing predictions with the models, and deriving mathematical models (symbolic representations of relationships that they find in graphs and table they build from data they gather in their experiments). The mathematical modeling of relationships between variables such as the number of gas particles, the temperature of a gas, the volume of the gas container, gas constants, and the pressure of the gas, helps students to progressively expand and derive the gas laws from experimental data. This mathematical modeling focus, helps students bridge the symbolic representations of the gas laws, to experimental data, to particle behavior.
The non-computer based activities ask students to apply ideas and relationships learned in class, extend the predictions of these relationships to new situations that they experience every day, and connect previous and upcoming concepts to their understanding of particle behavior (Kinetic Molecular Theory) and to broader cross cutting themes in science. Some of the broad cross cutting themes include building and using scientific models, systems thinking, data analysis, and change and equilibrium.
These activities will build a deep and intuitive sense of particle behavior that will extend readily to other chemistry topics. In particular, the behavior of particles in chemical reactions becomes easy to envision and predict the outcome of the interactions of molecules, even when the reactants are in solid or liquid form. This is because many of the concepts related to chemical reactions rely on an understanding of the number of molecules, volume, and temperature, and pressure.
Teacher Guide (pdf)
Standards
Next Generation Science Standards
- Physical Science
- [HS-PS2] Motion and Stability: Forces and Interactions
- NGSS Crosscutting Concept
- Patterns
- Systems
- Structure and Function
- NGSS Practice
- Analyzing Data
- Constructing Explanations, Designing Solutions
- Asking Questions, Defining Problems
- Using Models
- Arguing from Evidence
- Conducting Investigations
Computational Thinking in STEM
- Data Practices
- Analyzing Data
- Collecting Data
- Creating Data
- Manipulating Data
- Visualizing Data
- Modeling and Simulation Practices
- Assessing Computational Models
- Designing Computational Models
- Using Computational Models to Find and Test Solutions
- Using Computational Models to Understand a Concept
- Computational Problem Solving Practices
- Assessing Different Approaches/Solutions to a Problem
- Computer Programming
- Troubleshooting and Debugging
- Systems Thinking Practices
- Investigating a Complex System as a Whole
- Thinking in Levels
- Understanding the Relationships within a System
Credits
The 2019 version of this unit is developed by Umit Aslan (umitaslan@u.northwestern.edu) and Nicholas LaGrassa (nicholaslagrassa2023@u.northwestern.edu).
Acknowledgement
A majority of this unit is adopted from the earlier Connected Chemistry units developed by Uri Wilensky, Mike Stieff, Sharona Levy, and Michael Novak (see http://ccl.northwestern.edu/rp/mac/index.shtml for more details). Some elements are also taken from the Particulate Nature of the Matter unit developed by Corey Brady, Michael Novak, Nathan Holbert, and Firat Soylu (see http://ccl.northwestern.edu/rp/modelsim/index.shtml for more details).
We also thank undergraduate research assistants Aimee Moses, Carson Rogge, Sumit Chandra, and Mitchell Estberg for their contributions.
Underlying Lessons
- Lesson 1. I - Introduction
- Lesson 2. II - What is pressure?
- Lesson 3. III - Number and Pressure
- Lesson 4. IV - Temperature and Pressure
- Lesson 5. V - Volume and Pressure
- Lesson 6. VI - The Ideal Gas Law

Lesson 1 Overview
This lesson introduces the students a real world fixed-volume container with gas: an air duster can. An explanation of the contents of the air duster can requires an understanding of gas particle behavior, which students will develop throughout the unit. The students are asked to generate three types of explanations about the can: (1) a text-based explanation, (2) a sketch illustration, and (3) a computational model. They develop the third explanation in three sub-steps. First, they build a static representation of the gas particle system using a NetLogo particle sandbox model. Then, they define the behavior of gas particles (e.g., their movement, collisions) using a blocks-based modeling toolkit. In this step, they work with only a few particles. Lastly, they bring in their gas behaviors to the particle sandbox and make their static model dynamic.
Throughout this lesson, they learn the rules that govern their behaviors and interactions by adding the rules into the model one-by-one. While observing the consequences of “running” these rules and the resulting motion of the particles. In addition, gain a familiarity with a microscopic view of the system and with the NetLogo model interface they will use again in later activities. This familiarity is a critical learning goal in the first Activity, since the use of computer interface (buttons, sliders, switches, etc...) becomes progressively more sophisticated in future activities. Finally, students reflect on their models and modeling practices.
Lesson 1 Activities
- 1.1. What is an air duster?
- 1.2. What is inside the can?
- 1.3. Discussion: Let's talk about our sketches
- 1.4. Using computational modeling to constructing a static model of the air duster can
- 1.5. Discussion: Let's talk about our static models
- 1.6. How do the particles behave?
- 1.7. Testing our particle code with many particles
- 1.8. Discussion: How do the particles behave?
- 1.9. Reflecting on our models
1.0. Student Directions and Resources
Welcome to the first lesson of the Connected Chemistry Ideal Gas Laws unit!
In this unit, we will investigate what causes gas pressure, how it is measured, and how it is affected by the properties of the particles that make the gas and the characteristics of the container they are in. To achieve this goal, we will study gases
- at the macroscopic level by exploring real world objects such as basketballs, air duster cans, and basketballs.
- at the microscopic level by using computational models.

We will begin our exploration with an air duster can. This everyday object will help us understand:
- How do gases behave in a fixed volume container?
- What are computational models?
- How do we create them?
- Why do we need them?
- How are they related to scientific models?
1.1. What is an air duster?




Question 1.1.1
Question 1.1.2
Why would anyone even need an air duster? Write as many reasons as you would like to. If your answer to the previous question was  , try to guess.
, try to guess.
Question 1.1.3
How does an air duster work? What is inside the can? If you are not sure, just hypothesize please. Write as many possibilities as you can think of.
1.2. What is inside the can?
Let's watch the following video of someone cleverly "hacking" an air duster. This demonstration may give us a better idea on how it works.
Question 1.2.1
Compare the following two experiments? Why don't the papers move initially? Why do they move in the second experiment? Please elaborate (min. 2 sentences).


Question 1.2.2
 What happens when the person presses the valve after pumping air? Explain what happens both inside and outside the air duster. (min. 3 sentences)
What happens when the person presses the valve after pumping air? Explain what happens both inside and outside the air duster. (min. 3 sentences)
Question 1.2.3
Now please illustrate your previous answer using the sketching tool below. What happens when the person presses the valve after pumping air? Please do not spend more than 6 minutes on this task.
Note: You can omit the paper pieces in your drawing.
Warning!: The "Clear" button will clear the whole sketch! If you want to erase parts of your drawing, use the white colored pencil.

Question 1.2.4
Can you explain your sketch? Which kinds of shapes did you draw? Why? (min. 3 sentences).
1.3. Discussion: Let's talk about our sketches

Please set your computer aside briefly (do not close this page) and join the classroom discussion that your teacher is going to moderate.
Note: If you the discussion has not started yet, please answer the extra credit question below as you are waiting.
Question 1.3.1
If the discussion has not started yet, start answering this question: Can you think of objects similar to the air duster can? List as many as you can and explain how it is similar to the air duster.
Question 1.3.2
Before moving on, please reflect on the classroom discussion briefly. How did other groups' ideas compare to your group's idea? How has your thinking changed? Did you learn new things? Did you find yourself asking more questions? (min. 4 sentences).
1.4. Using computational modeling to constructing a static model of the air duster can
In this unit, we are going to work with a few fundamental assumptions about gases. The first of them is: gases are made up of many individual particles (molecules).
However, we cannot see the gas molecules inside the air duster can; they are too small to see with only our eyes 👀. Instead, we will use NetLogo 🔗 to develop a computational model to visualize the molecules inside the air duster can as the air is being pumped into it. NetLogo is a free programmable environment for building and running computational scientific models that simulate natural and social phenomena.
Scientific models 🔗 are used to explain and predict the behavior of real objects or systems and are used in a variety of scientific disciplines. They can be expressed in many different ways. For example, your written explanations and sketches can be considered as informal models of the gas behavior in the air duster can.
Below is a simple particle sandbox modeling toolkit. We can use this simple modeling toolkit to construct static systems that include basic particles and barriers. The short video above demonstrates how to use this tool.
Now let's re-create an approximation of our sketched models of the air duster can using the simple modeling toolkit below!
Please do not spend more than 6 minutes on this task.
Question 1.4.1
When you are done building your model, save it using the 
| File | Delete |
|---|---|
Question 1.4.2
Also take a screenshot of your model using the 
| File | Delete |
|---|---|
Question 1.4.3
How does this modeling toolkit compare to the sketching activity in the previous page? What are the similarities? What are the differences?
(min. 2 sentences).
1.5. Discussion: Let's talk about our static models

Again, please set your computer aside briefly (do not close this page) and join the classroom discussion that your teacher is going to moderate.
Note: If you the discussion has not started yet, please answer the extra credit question below as you are waiting.
Question 1.5.1
If the discussion has not started yet, answer this question: The sandbox model you just used is obviously very limited. It only has a small number of tools. If you were to extend it, what would you add? What kind of options would you give to the users? Why? (min. 2 ideas)
Question 1.5.2
Before moving on, please reflect on the classroom discussion briefly. How did other groups' ideas compared to your group's idea? How has your thinking changed? Did you learn new things? Did you find yourself asking more questions? (min. 2 sentences).
1.6. How do the particles behave?
The particle sandbox model allowed us to create simple gas molecules and place them inside containers. However, it did not allow us to see how the particles behaved. We can use computer models to animate the particles, too.
Below is another simple modeling toolkit that allows us to define the behavior of gas particles. For simplicity, this toolkit allows you to work only up to 4 particles. The short video on the right demonstrates how to use the blocks below the model to program the behavior of the particles. Please watch it carefully if you are having difficulty with the blocks.
A few quick points:
- Click
to reset the model and click
to run your model.
- Your code should always start with the
block, or the model will not know what to do.
- Your code will be performed by the particles continuously.
- For example, if you wrote that "each particle + moves zig-zag", each particle in the model will move one step forward doing a zig-zag movement and then move one more step forward the same way, and so on. This will keep going on as long as the GO button is pressed.
Now let's try to figure out how gas behave inside a container!
Please do not spend more than 6 minutes on this task.
Question 1.6.1
When you are satisfied with the way the particles behave, 
| File | Delete |
|---|---|
Question 1.6.2
Which types of blocks did you use? Please explain your reasoning for each block.
Example: block: I used the "moves ____" block | because: I think the molecules moves so and so ....
Question 1.6.3
Please reflect on your modeling process: What was easy? What was hard? (min. 2 sentences)
Note: If you have time, also reflect on what was enjoyable and what was not enjoyable.
1.7. Testing our particle code with many particles
Now we can put our static particle sandbox model and our particle behavior block codes together. Let's use the combined modeling toolkit below to:
- Load your static model design from Page 4* using the
button.
- Re-create your blocks code and run it within your sandbox model.
- If the model does not behave as you anticipated, change your experiment design (e.g., add more particles, walls) or blocks-code to manipulate your model.
Note: If you don't remember the code you wrote in the previous step, you should be able to see a link to your blocks code screenshot below the modeling toolkit.
* If you did not save your design, try to recreate it as best as you can. But this time, don't forget to save it.
Question 1.7.1
Did you have to change anything in this step (e.g., particles, walls, block codes)? If yes, please explain each change briefly.
Question 1.7.2
Did your air-duster-can model work as you expected? Did you need to change anything? Explain briefly (min. 2 sentences)
1.8. Discussion: How do the particles behave?
 One last time, please set your computer aside briefly (do not close this page) and join the classroom discussion that your teacher is going to moderate.
One last time, please set your computer aside briefly (do not close this page) and join the classroom discussion that your teacher is going to moderate.
Note: If you the discussion has not started yet, please answer the extra credit question below as you are waiting.
Question 1.8.1
If the classroom discussion has not started yet, start answering the following question: If you were to be able to add new code blocks to this computational model, what would you add? Choose a title for each block and explain in 1-2 sentences.
Question 1.8.2
Before moving on, please reflect on the classroom discussion briefly. How did other groups' ideas compared to your group's idea? How has your thinking changed? Did you learn new things? Did you find yourself asking more questions? (min. 2 sentences).
1.9. Reflecting on our models
In this final section, we will compare all three of our models (written, sketch, and computational).
Question 1.9.1
How does each of your models (textual, sketch, computational) compare to what happens inside the actual air duster can?
Question 1.9.2
Do you think your computational model actually represents what is happening in real life? Please elaborate (min. 2 sentences).
Question 1.9.3
Optional follow-up question
If you were to explain your final understanding of how the “air duster can” works in real life as a grand, coherent theory, how would you express it? (no more than 3 sentences).

Lesson 2 Overview
In this lesson, the students learn the basic assumptions of the Kinetic Molecular Theory (KMT) and how they help us conceptualize "pressure as a macro-level property that emerges from the micro-level interactions between many gas particles".
The lesson starts with the basic assumptions of KMT [1]:
1. The gas is composed of a large number of identical molecules moving in random directions, separated by distances that are large compared with their size.
2. Collision between gas particles occur like collisions between billiard balls (i.e. elastic collision). Otherwise, they do not interact. There are no attractive or repulsive forces between the particles.
3. Any energy the particles have is because of their motion only (i.e. kinetic energy).
4. These assumptions are simplifications that describe a theoretical "ideal gas". Most real gases behave qualitatively like an ideal gas.
The students reflect on the assumptions of the KMT and their own gas particle models from Lesson 1.
Then, the students are given an introductory definition of pressure. They are guided through an investigation of this definition using a simple NetLogo model of the bike tire. They observe the effects of adding particles through a valve on the pressure of the tire. They also consider the trade-offs of making simplifications when constructing models of systems.
The lesson ends with a "discrepant event" activity to stimulate transfer: "Can blow up a balloon inside a bottle?".
[1] The students are not expected to learn mathematical representations of the KMT as it is too complex for this grade level.
Lesson 2 Activities
- 2.1. Kinetic Molecular Theory
- 2.2. The computational bike-tire model
- 2.3. What is pressure?
- 2.4. Discussion: What causes pressure inside the bike tire?
- 2.5. Stability, fluctuations, and change in pressure
- 2.6. Using models in scientific inquiry: simplifications vs. the real world
- 2.7. Applying our knowledge to another phenomenon: The balloon in the bottle experiment
2.0. Student Directions and Resources
In this lesson, you will use a scientific model similar to the one you developed in the previous lesson. Using this model, you will observe the effects of pumping air into a bike tire.

The simple bike tire model will help us understand:
- Learning about the Kinetic Molecular Theory and its main assumptions
- Defining pressure (P) in a gas container
- Thinking about the role of gas pressure in real-life objects and events
- Considering the trade-offs of making simplifications when constructing computer-based models
2.1. Kinetic Molecular Theory
In Lesson 1, we tried to hypothesize about how gas particles behave in a container. We did so by writing our hypotheses verbally, sketching, developing static computational representations, and finally defining the behavior of the gas particles within a block-based programming environment.
The Kinetic Molecular Theory (KMT) is the scientific theory that is used to explain and predict the behavior of different objects that use air pressure to function such as these:



The main assumptions of Kinetic Molecular Theory (KMT) are the following:
- A gas is composed of a large number of identical molecules moving in random directions, separated by distances that are large compared with their size.
- Collision between gas particles occur like collisions between billiard balls (i.e. the total energy is conserved; see elastic collision 🔗). Otherwise, they do not interact. There are no attractive or repulsive forces between the particles.
- Any energy the particles have is because of their motion only (i.e. kinetic energy).
- These assumptions are simplifications that describe a theoretical "ideal gas". Most real gases behave qualitatively like an ideal gas.


Before we move on to the implications of KMT, let's first reflect on how these assumptions compare to our gas particle models from the Lesson 1.
Question 2.1.1
How do the assumptions of the KMT compare to the block-based code of your model? What are the differences? What are the similarities? (min 2 sentences)
Question 2.1.2
Why would it be important to know how gas particles behave inside a container? If you are not sure, try to hypothesize (min 2 sentences).
2.2. The computational bike-tire model
Study a physical bike tire and a pump (or equivalent objects chosen by your teacher) in the classroom. Try to observe what happens when you pump air into the tire. As you are doing this, keep the assumptions of KMT in your mind.
Then, familiarize yourselves with the simple computational bike-tire model below. To run it, first click the 

For now, just experiment with the model freely as you experimented with the physical bike tire and pump. Observe what happens when you run the model with different settings. Please do not spend more than 4 minutes on this task.
Question 2.2.1
How does this model compare to a real (physical) bike tire? What is missing? What is common? (min 2 sentences)
Question 2.2.2
How does this model compare to your air duster can model from Lesson 1? What is missing? What is common? (min 2 sentences)
Question 2.2.3
Did you try to add more particles? If no, scroll up and try to add more particles using the 
Tip: Using the  option may help.
option may help.
2.3. What is pressure?

(P)ressure = (F)orce / Surface (A)rea
This means that the pressure on a surface depends both on the force that is applied to the surface and the size of the surface. A larger force on a surface leads to larger pressure. A larger surface with the same force against it leads to a smaller pressure.
What does this definition of pressure imply for our Bike Tire model? What constitutes the "surface area"? Where does the force come from? How do we calculate the pressure in a fixed volume gas container like the one in our model?
We will use our simple Bike Tire model to find answers to these questions. Run the model once or twice without changing any parameters. Just observe the "pressure over time" plot for a while (≈30 ticks). Then answer the questions below.
Please do not spend more than 4 minutes with this task.
Question 2.3.1
How does the "pressure over time" plot change when you run the model with 50 particles? Describe each distinct pattern you observe. (min 2 sentences)
Question 2.3.2
If you did not change the parameters, you should have observed a plot similar to the one below. Find a word to describe the part that is marked with red? Also hypothesize: Why might we observe such a pattern? (min 3 sentences)
Question 2.3.3
How do you think the value of "pressure" is calculated inside this bike tire? (min. 3 sentences)
Tip: Remember that pressure (P) is defined as F/A (force divided by the surface area). Try to think about these two questions: (1) "what is the surface area in this model?" and (2) "what applies force to the surface area in this model"?
2.4. Discussion: What causes pressure inside the bike tire?

Please set your computer aside briefly (do not close this page) and join the classroom discussion that your teacher is going to moderate.
Note: If your teacher did not initiate the discussion yet, please start answering the first question below as you are waiting.
Question 2.4.1
If the discussion has not started yet, start answering this question: Can you think of any objects that take advantage of gas pressure similar to the bike tire? List as many as you can and explain why.
Question 2.4.2
Before moving on, please reflect on the classroom discussion briefly: What creates pressure inside a gas container? Where does the force come from? Why do we observe the fluctuations (i.e. oscillations or relatively stable up-and-down changes) in the image below? (min. 3 sentences).
2.5. Stability, fluctuations, and change in pressure
In the case of gas particles in a container (e.g., a real bike tire, the air duster can, and the Bike Tire model below) the pressure of the system is created by the particles hitting the walls of the container.
The pressure at a given instant is calculated as the total force applied by the particles hitting the walls at a given time and the surface area is the area of the walls.
That is also why we observe the fluctuations in the "pressure over time" plot: at a given tick, slightly different number of particles may hit the walls, and the total force applied by them might be slightly different.
Now let's explore what is the difference between the fluctuations in the plot, changes in pressure, and the stability of the system:
- Run the model with 50 particles by clicking the
button, and then clicking the
button.
- Wait until the system stabilizes (≈20 ticks).
- Add 150 more particles using the
button three times.
- Observe the changes in the system until the system stabilizes again.
Question 2.5.1
When you click the 
Question 2.5.2
When we first add new particles (or pump air inside our imaginary bike tire), we see an initial spike in the pressure but then the system stabilizes at a lower pressure. One such spike is marked with red in the image below. The stable state is marked with green. Why does this happen? Explain the events. (min. 2 sentences)
2.6. Using models in scientific inquiry: simplifications vs. the real world

Before ending this lesson, let's reflect on the differences between the two and why might we (and scientists) want to use such computational models.
Question 2.6.1
List any simplifications that you can think of in the bike tire model compared to a real world bike-tire. (min 2. simplifications)
Question 2.6.2
In the model, the bike tire does not change inflate (increase its volume) when air particles are pumped into it. Why do you think this simplification was made?
Question 2.6.3
Why would we (and scientists) need to build models that are less detailed than the real world? Is it out of necessity? Do these simplifications offer any advantages? (min. 2 sentences)
2.7. Applying our knowledge to another phenomenon: The balloon in the bottle experiment
Please set your computer aside briefly (do not close this page) and join the classroom discussion and the physical experiment that your teacher is going to moderate.


Question 2.7.1
Before trying the experiment in real life, discuss this question with your group member(s) and summarize your discussion below? Come up with at least one hypothetical answer and explain why (min. 3 sentences).
Question 2.7.2
After the experiment, reflect on your initial answers? Did you guess correctly? Were you wrong? (min. 2 sentences).
Question 2.7.3
How does the balloon-bottle system compare to our explorations with the bike tire model? Please explain in terms of the underlying gas particle behavior (min. 2 sentences).

Lesson 3 Overview
This lesson introduces a new tool called CODAP, which automates data collection and plotting with the model. They use CODAP to investigate the quantitative relationship between the number of particles in a container and the pressure inside. They sort and clean their data, then create a graph and find a trend-line. Students use the trend-line equation to predict and test their prediction for new pressure values.
Lesson 3 Activities
- 3.1. Our experimental setup: the bike-tire model
- 3.2. Our experimental setup: the CODAP data analysis workbench
- 3.3. Let's talk about our experimental designs
- 3.4. Conducting our first computational experiment with CODAP
- 3.5. Drawing conclusions from data: finding a quantitative relationship
- 3.6. Putting our mathematical model to use
3.0. Student Directions and Resources
In the previous two lessons, we qualitatively explored:
- the behavior of gas particles inside fixed volume containers
- and how the simultaneous behavior of many gas particles at micro-level result in a macro-level property, pressure.

In this lesson, we are going to start developing quantitative relationships between the macro-level properties of gasses. To do so, we will use a slightly different version of the bike tire model from the lesson 2 and a quantitative data analysis application called CODAP.
The goals of this lesson are:
- What is the relationship between the number of particles in a gas container and gas pressure?
- How can we design experiments within computational models to collect quantitative data?
- How can we analyze quantitative data using CODAP to determine a mathematical relationship between our two variables?
3.1. Our experimental setup: the bike-tire model
Before starting our computational experiments, let us familiarize ourselves with our experimental setup. The first component of our experimental setup is a slightly modified version of the Bike Tire model from the previous lesson.
- There is no "add particles" button anymore. We will decide the number of particles inside the bike tire before running each experiment.
- There is a new
slider. This slider will help us run experiments until the system stabilizes (e.g., the model will stop).

- Set the "number-of-particles" parameter to 100 and the "ticks-to-run" parameter to 15.
- Click the
button to set-up the experiment.
- Then
button to run the experiment.
- Click the
- Once the experiment is completed, move your mouse over the plot (as shown on the right) and see how the pressure has changed over time. Note down the final pressure of the system.
- Repeat the same procedure with 200 particles and 15 ticks. Note the resulting pressure.
- Repeat the same procedure with 300 particles and 15 ticks. Note the resulting pressure.
- Answer the questions below the model.
Question 3.1.1
Record your measurements in the table below.
Question 3.1.2
It may be too hard to notice trends in data by just looking at raw numbers. Mark your data points on the following sketch in order to see if there is any correlation 🔗 between our two variables (x = number of particles, y = pressure). Do not worry about perfect precision when you mark the points.

Question 3.1.3
Based on the data you just collected, what happens to the pressure when there are more particles in the box?
Decreases
Stays the same
Other
Question 3.1.4
The fluctuations in the plot pose a practical problem to solve? Even though the pressure stabilizes, each reading at the stable state might be slightly different. Observe the following comparison. How should we record our data to make sure that our findings are reliable? (min 2 sentences)

3.2. Our experimental setup: the CODAP data analysis workbench
In the previous lesson, we ran 3 experiments and then tried to plot the data by hand. Even with just three experiments, we started noticing trends. However, we also noticed two important issues:
-
Reliability issue: The particles' random behavior may lead to fluctuations in our final pressure value.
-
Practicality issue: We might not be able to precisely plot the data by our hands.
Scientists try to overcome such issues by using an approach called "statistical mechanics 🔗". To put it simply, they collect lots of data and then use statistical methods to determine mathematical relationships between variables.
Below, you will see a CODAP workbench. CODAP is a web-based data analysis platform that will make it much easier for us to run many experiments at once. It will also make it much easier to plot our data and find out mathematical relationships between the variables.
Let's begin with familiarizing ourselves with the CODAP environment:
- Run three experiments for 15 ticks: with 100 particles, with 200 particles, and with 300 particles. (p.s.: you can speed up the model to get the results more quickly)
- Observe how the results of each experiment is automatically transferred to the "Experiment results" table on the right.
- Drag the num_particles variable to the x-axis of the plot plot as shown in the GIF on the right.
- Drag the last_pressure_value variable to the y-axis of the plot plot as shown in the GIF on the right.
- Observe the resulting plot. Then answer the questions below the CODAP workbench.
Question 3.2.1
How do your hand-collected data points and your hand-drawn plot compare to the ones you created with CODAP? (write min. 1 similarity and 1 difference).
Question 3.2.2
How confident are you with your findings? Do you think the relationship you found may change if we conduct more experiments? Do you think it will stay the same? Explain how & why? (min 2 sentences)
Question 3.2.3
In the next page, you are going to conduct your first computational experiment. To keep things simple in this lesson, you will design an experiment for a pre-determined research question:
| Dependent variable: | (P)ressure |
| Independent variable: | (N) umber of particles |
| Research question: |
Is there any mathematical relationship between these two variables? If yes, what is the nature of this relationship? |
When designing your first computational experiment using the table above, you should have the following considerations in mind:
- Collect sufficient number of data points to find a reliable answer to the research question.
- Test different values for the independent variable (N) to find a reliable answer to the research question (min. 5 different values).
- Enter each value for independent variable in a new row.
- Add more rows by clicking any of the the
buttons.
- Design an experiment that can be practically conducted within CODAP.
Note: You will run this experiment within the CODAP workbench in the next page.
3.3. Let's talk about our experimental designs
 Please set your computer aside briefly (do not close this page) and join the classroom discussion that your teacher is going to moderate.
Please set your computer aside briefly (do not close this page) and join the classroom discussion that your teacher is going to moderate.
Note: If your teacher did not initiate the discussion yet, you can start answering the first four questions below as you are waiting.
Question 3.3.1
If the discussion has not started yet, start answering the following question (and the next 3 questions): What is an experiment? Why do we conduct experiments?
Question 3.3.2
If the discussion has not started yet, please answer the following question: Can you list a few experiments that you heard about outside of school (e.g., news, internet, etc.)? How would you compare those experiments with the experiments we are conducting in this unit? (min. 2 sentences)
Question 3.3.3
Before moving on, please reflect on the classroom discussion briefly: (1) What are the characteristics of a good, practical computational experiment? (2) Which initial conditions we need? Why? (3) How many repetitions do we need? Why ?
3.4. Conducting our first computational experiment with CODAP
Now let's go ahead and conduct our fist computational experiment within CODAP!!!
Note: If you do not remember the exact details, you can see your initial experimental design below the CODAP window.
Also note: If you changed your mind after the classroom discussion, feel free to make changes to your experimental design.
A final note: Do not forget to drag variable names to the axes of your plot widget as you did in the Page 2.
Question 3.4.1
Did you make any changes to your initial experimental design after the classroom discussion? If yes, explain briefly.
Question 3.4.2
You collected 3 data points by hand, 6 data points within CODAP as a pre-experiment, and (hopefully) many more data points during your actual experiment.
Can you summarize the result of your experiment verbally? What is your finding? Is there a relationship between your dependent variable (Pressure) and your independent variable (Number of Particules)? (min 2. sentences)
Question 3.4.3

- Click the hamburger menu (
) icon on he top-left corner of the CODAP window.
- Click Save (
).
- Choose the Local File option (
)
- Click Download (
).
Upload your CODAP file using the "Browse..." button below.
| File | Delete |
|---|---|
3.5. Drawing conclusions from data: finding a quantitative relationship
So far, we collected many data points from the Bike Tire model, we plotted them, and saw a consistent relationship. We stated our findings verbally such as "the more particles in the box, the higher is the pressure".
However, verbal statements cannot help us answer questions such as: "What happens if I add 10 more particles to the box?" or "Approximately how many particles are inside the box if the pressure is 440?"
To answer such quantitative questions, we need to develop mathematical equations.

- Load your CODAP savefile by clicking CODAP's hamburger menu (
) and then clicking "Open".
- Open your file from the "Local File" section. You should have all your data back in the "Experiment Results" table, as well as your plot.
- Click anywhere on the plot, and then click the ruler icon (
).
- Click the
option.
- A line with three anchor points will appear. Move the line as shown on the right to fit the data as best as you can.
- Note the linear equation 🔗 (with yellow background) that CODAP generates for us.
Question 3.5.1
A linear equation, like the one you developed in CODAP, takes the form y = mx + b where:
- y is your dependent variable (Pressure)
- x is your independent variable (Number of Particles)
- m (or the slope of the moveable line) represents the rate of change (e.g., pressure per particle).
- and b is where your line intercepts the y-axis. To make things even simpler, we can ignore this number for now.
What is the linear equation you developed in CODAP from data? Use P instead of y and N instead of x. Write it in the following form: P = m x N (for example, P = 1.5 x N).
Question 3.5.2
Also export an image of your CODAP plot. Please download your plot and upload it using the "Browse" button below
Here's how you can do it:
- Click anywhere on the "Experiment Results" table, a sidebar will pop-up on the right.
- Click the last icon (
).
- Choose the "Local Data" option on the left and click "Download".
| File | Delete |
|---|---|
Question 3.5.3
Save the latest version of your CODAP file and upload it again.
| File | Delete |
|---|---|
3.6. Putting our mathematical model to use

- We analyzed a real world phenomenon using a computational model.
- We designed an experiment to find out the relationship between two variables.
- We collected data and plotted our data points on a graph.
- We used a computational data analysis tool to develop a mathematical equation.
We should now test the validity of our Pressure-Number equation through further experimentation! You can skip directly to the questions below.
Question 3.6.1
Using your Pressure-Number equation, calculate approximately how many particles you would need to have in the box to reach a pressure of about 500.
Question 3.6.2
Test your prediction in the model by changing the initial number of particles. How many particles did you need to get the pressure to stabilize around 500?
Question 3.6.3
Did your mathematical model predict the answer correctly? Were there any differences? If yes, what might have contributed to any differences between your prediction and the model?
Question 3.6.4
Do you think this experiment validated your mathematical model? If your answer is "yes", explain why? If you say "no", explain what more we need to do. (min. 2 sentences)

Lesson 4 Overview
This lesson introduces a computer model that now includes the effect of warming up and cooling down the bike tire walls. They use this model to examine the relationships between speed of particles and the temperature of the gas as well as between temperature and pressure. Students use CODAP to collect data and then find a linear equation of the relationship between temperature and pressure. They use the equation to make predictions about what the pressure will be for temperature conditions.
Lesson 4 Activities
- 4.1. Why does the balloon expand?
- 4.2. Let's talk about our balloon sketches
- 4.3. Our experimental setup: the "warm up -- cool down" model
- 4.4. Using CODAP to develop a mathematical Pressure-Temperature model
- 4.5. Validating our mathematical model
4.0. Student Directions and Resources
In the previous two lessons, we used computational models of a bike tire to:
- describe how "pressure" as a macro-level property emerges from the micro-level interactions between the gas particles and the container's walls
- find a relationship between two variables, the number of particles and pressure, by conducting computational experiments and doing statistical analysis.


In this lesson, we are going to explore the relationship between temperature and pressure. To do so, we are going to use a new NetLogo model and the CODAP data analysis platform.
The goals of this lesson are:
- Defining temperature in a gas container.
- Understanding the relationship between gas particles' movement (kinetic energy) and gas temperature.
- Analyzing the relationship between gas temperature (independent variable) and gas pressure (dependent variable).
- Developing a mathematical model that defines the relationship between gas temperature and pressure quantitatively.
4.1. Why does the balloon expand?

- The experimenter places a blown balloon inside liquid nitrogen*.
- The balloon shrinks while contacting the liquid nitrogen.
- He takes the shrunk balloon out and holds it in his hands.
- The balloon automatically expands.
Why does the balloon expand? Let's hypothesize.
*Liquid nitrogen is a very cold substance used in food industry to preserve food by freezing it quickly. It is also used in medicine to treat skin conditions.
Question 4.1.1
What is the difference when the balloon is contacting liquid nitrogen and when it is outside of the bowl? Draw a sketch for each condition. Things to consider: what is inside the balloon? how do the outside conditions affect the interior of the balloon? (please spend no more than 6 minutes on this task).
Note: please use colors other than black to differentiate with the balloon outline.

Question 4.1.2
Please explain your sketch verbally. (min. 3 sentences)
- Which shapes did you draw on the left? Why?
- Which shapes did you draw on the right? Why?
Question 4.1.3
Did "gas pressure" factor into your thinking? If yes, please elaborate. If no, why? (min. 2 sentences)
Question 4.1.4
If you were to develop a NetLogo model to explore this phenomena, how would you design it? Explain verbally (min 3 sentences/ideas):
- What would the model's view look like?
- What kind of elements would be in the model?
- What kind of tools would you have (e.g., sliders, buttons)?
4.2. Let's talk about our balloon sketches
 Please set your computer aside briefly (do not close this page) and join the classroom discussion that your teacher is going to moderate.
Please set your computer aside briefly (do not close this page) and join the classroom discussion that your teacher is going to moderate.
Note: If your teacher did not initiate the discussion yet, you can start answering the first four questions below as you are waiting.
Question 4.2.1
If the discussion has not started yet, start answering the following question (and the next 3 questions): Can you think of other real world objects that shrink due to outside temperature (except tires and ballons)?
Question 4.2.2

Question 4.2.3
Before moving on, please reflect on the classroom discussion briefly: (1) How did your sketch compared to the other groups' sketches? (2) What were the similarities? (3) What were the differences? (min 2. sentences)
4.3. Our experimental setup: the "warm up -- cool down" model
Let us begin our exploration of the relationship between gas pressure and gas temperature with another NetLogo model. In this model, we have a fixed-volume gas container similar to our previous Bike Tire model. However, this model allows us to warm up and cool down the walls of the container.
When a particle hits the wall, two things may happen:
- If it has more kinetic energy than the energy of the wall, it will loose some of its energy.
- the loss of energy is dependent on the difference between the particle's energy and the wall's energy.
- If it has less energy than the energy of the wall, it will gain some energy.
- the gain of energy is dependent on the difference between the particle's energy and the wall's energy.
- Particles only have kinetic energy. The higher a particle's kinetic energy, the faster it moves.
- a particle will speed up if it gains energy from the wall
- a particle will slow down if it looses energy to the wall
Now begin exploring the model:
- Run the model by clicking "setup" and then clicking "go".
- Wait until all three plots stabilize.
- Warm up the walls (at least 6).
- Observe the changes in plots.
- Repeat the same steps, but this time cool down the walls.
Some quick notes: The temperature of a gas is related to the average speed of the particles. When the average particle speed increases, the temperature also increases. However, this is not a linear relationship. Gas temperature is proportional to the square of the average particle speed. For example, if you double the average speed, you will quadruple the temperature.
Even though temperature and average particle speed are not directly proportional, when one increases the other will too. This means we can still use them to make comparisons and develop mathematical models.
Question 4.3.1
What happens to the particles when you warm up the walls of the container? Briefly describe the events you observe. (min. 2 sentences)
Quick tip: You can use the 
Question 4.3.2
What happens to the particles when you cool down the walls of the container? Briefly describe the events you observe. (min. 2 sentences)
Quick tip: You can use the 
Question 4.3.3
What changes did you observe in the plots? Briefly describe how each plot changes when you warm up the walls. (min. 3 sentences)
Question 4.3.4
In the next page, you are going to conduct another computational experiment. Once again, you will conduct an experiment to answer a pre-determined research question:
| Dependent variable: | (P)ressure |
| Independent variable: | (T)emperature |
| Research question: |
Is there any mathematical relationship between these two variables? If yes, what is the nature of this relationship? |
Note: Remember that you cannot manipulate the gas temperature directly. You can manipulate it only indirectly by manipulating the "outside energy" parameter. Hence, the table below does not have a "temperature" column.
Also note: Remember the experiment you ran in the previous lesson and also remember that you will run this experiment within CODAP in the next page.
4.4. Using CODAP to develop a mathematical Pressure-Temperature model
Now let's go ahead and conduct our experiment within CODAP!!!
Note: If you do not remember the exact details, you can see your experimental design below the CODAP window. If you are not sure about your experimental design, consult your teacher. Here are a few considerations to keep in mind:
- Run each experiment long enough so that all three plots stabilize before your model reports the data.
- Keep non-involved parameters (e.g., number of particles, ticks-to-run) fixed at all experiments.
- Run at least 3 trials (repetitions) for each combination.
- Try at least 5 different values for the independent variable (temperature/outside-energy).
- Speed up the model to conduct the experiments as fast as possible.

If you do not remember exactly, here is how to do it:
- Load your CODAP savefile by clicking CODAP's hamburger menu (
) and then clicking "Open".
- Open your file from the "Local File" section. You should have all your data back in the "Experiment Results" table, as well as your plot.
- Click anywhere on the plot, and then click the ruler icon (
).
- Click the
option.
- A line with three anchor points will appear. Move the line as shown on the right to fit the data as best as you can.
- Note the linear equation 🔗 (with yellow background) that CODAP generates for us.
Question 4.4.1
First and foremost, save your CODAP experiment and upload it using the "Browse" button below. You can do it as follows:
- Click the hamburger menu (
) icon on he top-left corner of the CODAP window.
- Click Save (
).
- Choose the Local File option (
)
- Click Download (
).
| File | Delete |
|---|---|
Question 4.4.2
What is the mathematical equation you found?
Note: Remember that you can omit the last part of the equation (b, in y = mx + b).
4.5. Validating our mathematical model
Question 4.5.1
According to your mathematical model, what would be the pressure if your gas temperature was about 200 degrees?
Question 4.5.2
Given that you cannot set the temperature directly in this model, how can we test the validity of your prediction? Briefly describe your strategy. (min. 2 sentences).
Question 4.5.3
If you observe a pressure of 170, what should be gas temperature?
Question 4.5.4
Were you able to validate your mathematical model? Explain why and how. (min. 2 sentences).
Question 4.5.5
Optional question if you finished the activities early: Would your answer to the "balloon-in-liquid-nitrogen" experiment change after this lesson? If no, explain why. If yes, explain how. (min. 2 sentences)
Question 4.5.6
Optional question if you finished the activities early: Would you change your sketch, too? If yes, go ahead and draw a new one


Lesson 5 Overview
This lesson introduces a computer model that allows them to change the location of one of the walls of the container, hence experiment with different volumes. They use this model to examine the relationships between container volume and pressure. Students use CODAP to collect data and then find a mathematical equation of the relationship between volume and pressure. They use the equation to make predictions about what the pressure will be for different volumes.
Lesson 5 Activities
- 5.1. Why does the marshmallow expand?
- 5.2. Our experimental setup: the virtual syringe model
- 5.3. It's CODAP Time!
- 5.4. Testing the validity of our mathematical model
5.0. Student Directions and Resources
In Lesson 3, we explored the relationship between the number of gas particles in a container and pressure. We kept other factors (temperature and volume) constant.
In Lesson 4, we explored the relationship between gas temperature and pressure. We kept other factors (number of particles and volume) constant.

In this lesson, we are going to explore the relationship between volume and pressure.
The goals of this lesson are:
- Analyzing the relationship between container volume (independent variable) and gas pressure (dependent variable).
- Developing a mathematical model to express the relationship between container volume and gas pressure.
5.1. Why does the marshmallow expand?

- The experimenter places a marshmallow inside an unsealed syringe.
- He pushes the plunger all the way until the marshmallow.
- He seals the syringe with his fingers.
- He pulls the plunger all the way
- The marshmallow expands.
Why does the marshmallow expand? Let's hypothesize.
Note: If your teacher has syringes (and maybe even marshmallows), you should try to conduct this experiment yourselves.
Question 5.1.1
What is the difference when the plunger is pushed all the way and when it is pulled all the way? Draw a sketch for each condition. (please spend no more than 6 minutes on this task).
Note: please use colors other than black to differentiate with the balloon outline.

Question 5.1.2
Please explain your sketch verbally (min. 3 sentences)
Question 5.1.3
Did "gas pressure" factor into your thinking? If yes, please elaborate. If no, why? (min. 2 sentences)
Question 5.1.4
Why do you think a marshmallow is used in this experiment? What would happen if we used a piece of wood instead?
5.2. Our experimental setup: the virtual syringe model
The models we used in the previous activities did not let us change the volume of the container. However, many gas containers, like balloons and syringes, grow and shrink. In this lesson, we are going to explore the relationship between container volume and pressure. To do so, we will use another slightly different model. This model will allow us to simulate a syringe; it will allow us to chance the position of a wall, so that we can increase and decrease the volume.
Begin experimenting with your model and explore the relationship between your dependent variable (pressure) and your independent variable (volume). Conduct a preliminary experiment as follows:
- Run the model with the default parameters (initial wall position = 30).
- Wait for pressure to stabilize. Take note. Also note the volume of the container.
- Move the wall to the right at least 10 units above 30 (higher volume).
- Wait for pressure to stabilize. Take note. Also note the volume of the container.
- Move the wall to the left at least 10 units below 30 (lower volume).
- Wait for pressure to stabilize. Take note. Also note the volume of the container.
Record the changes in the data table below.
Note: We already know that increasing the number of particles increase pressure. So, do not change the number of particles in your trials. Otherwise, your data may mislead you.
Question 5.2.1
Record the results of your preliminary experiment below.
Question 5.2.2
Mark your data points in the plot below.

Question 5.2.3
What kind of a relationship between volume-pressure do you observe from these three data points? Is it similar to our previous explorations (number-pressure, temperature-pressure)? Is it different? Please elaborate. (min 3. sentences).
Question 5.2.4
In the next page, you will conduct your last experiment in CODAP in this unit. Design your experiment using the table below:
| Dependent variable: | (P)ressure |
| Independent variable: | (V) olume |
| Research question: |
Is there any relationship between these two variables? If yes, what is the mathematical nature of this relationship? |
Note: Once again, we cannot directly set the volume of the container. Instead, determine values for the "wall position" parameter.
5.3. It's CODAP Time!
Now let's go ahead and conduct our final computational experiment within CODAP!!!
Note: If you do not remember the exact details, you can see your initial experimental design below the CODAP window. If you are not sure about your experimental design, consult your teacher before starting.
- Run each experiment long enough so that pressure stabilizes before your model reports the data.
- Keep non-involved parameters (e.g., number of particles, ticks-to-run) fixed at all experiments.
- Run at least 3 trials (repetitions) for each combination.
- Try at least 5 different values for the independent variable (volume/wall-position).
- Speed up the model to conduct the experiments as fast as possible.
Question 5.3.1
First and foremost, save your CODAP experiment and upload it using the "Browse" button below. You can do it as follows:
- Click the hamburger menu (
) icon on he top-left corner of the CODAP window.
- Click Save (
).
- Choose the Local File option (
)
- Click Download (
).
| File | Delete |
|---|---|
Question 5.3.2

You can export a plot in CODAP as an image:
- Click anywhere on the plot.
- From the side menu, click the camera icon.
- Click the "Export Image" item.
- A pop-up window will open. Choose the "Local File" option and then click "Download"
| File | Delete |
|---|---|
Question 5.3.3
At this point, if you collected enough data, you must have noticed that:
- pressure decreases as volume increases
- resulting plot looks more like an arc than a straight line
Both of these findings are different than our previous two explorations.
Why do you think we observe this arc-like plot? (min. 2 sentences).
Question 5.3.4

The specific type of relationship we are observing can be expressed through a mathematical form as follows: y = m / x, where m is a constant coefficient.
On the other hand, we can use CODAP's "Plotted Function" tool to approximate a mathematical function that fits our data:
- Click anywhere on the plot.
- In the opening window, click the "Plotted Function" option.
- A bar with caption f() will appear on the top of the plot.
- Click the function bar and write "10000 / volume" as your plotted function. This means your function is P = 10000 / V.
- Repeat this step until you find a coefficient value that
What was the coefficient that fit your data the best?
Question 5.3.5
What is your mathematical model (equation) that explains your data the best?
Write it as: Pressure = coefficient / Volume
5.4. Testing the validity of our mathematical model
As usual, let's put our mathematical model to a test and if our inverse plotted function approach paid-off!
Question 5.4.1
According to your mathematical model, if we observe a pressure of 250, what would our volume be (approximately)?
Question 5.4.2
Were you able to validate your prediction within the model? Explain. (min 2. sentences)
Question 5.4.3
According to your mathematical model, what would pressure be if our container's volume is 5500?
Question 5.4.4
If you tried to validate your prediction with the model, you must have noticed that the largest volume allowed is 2970. Hence, we cannot test our prediction with the current version of the model.
Still, how confident are you in your prediction? Do you think your model would still be useful in situations that are not easily testable? Elaborate. (min. 3 sentences)
Question 5.4.5

Now that you completed your computational experiment and developed a mathematical model of Pressure-Volume in a gas container, did your thinking about this phenomenon change?
Please explain your final understanding verbally. But more importantly, please elaborate how your understanding is informed by your mathematical model? (min 3 sentences).

Lesson 6 Overview
This lesson asks the students to connect all their previous gas particle investigations. In contrast to previous lessons, they do not conduct any model-based explorations. Instead, they work on connecting the three gas equations they developed in the previous lesson and they try to apply those models to a real-world gas-related problem. They are then introduced to the Ideal Gas law, PV = nRT, which is a combination of the three models.
Lesson 6 Activities
- 6.1. Let's think about the air duster can again
- 6.2. Putting the pieces together: developing an ideal gas equation
- 6.3. Let's talk about our ideal gas theories
- 6.4. The ideal gas law: making the theory work
6.0. Student Directions and Resources

- We observed a macro-level gas phenomenon (air duster can) and we tried to reason about the underlying micro-level events such as:
- What is a gas made up of?
- How do gas particles move in space?
- How do gas particles interact with each other and the walls of the container?
- We tried to qualitatively understand how micro-level interactions among gas particles lead to an important macro-level property: pressure.
- What is kinetic molecular theory?
- What is an ideal gas?
- We qualitatively and quantitatively explored the relationship between three variables and gas pressure: number of particles, gas temperature, container volume.
- How can we use computational models to study the behavior of gasses?
- How can we conduct computational experiments to: collect data, analyze data, and develop mathematical models?
- How do we validate our mathematical models?
- In what ways our mathematical models help us reason about real-world phenomena that involves gas pressure?



In this final lesson, we will reflect on our hard work and try to put together all three mathematical models, as well as our understanding of the behavior of gas particles, to develop a coherent theory of ideal gases.
6.1. Let's think about the air duster can again
We started this unit with an exploration on how the "air duster can" works. Let's revisit the air duster can again, but this time, about another interesting aspect of air duster cans (and all other spray cans), the warnings:

Can we use the knowledge we constructed through previous 5 lessons to explain why we need these warning texts on spray cans?
Question 6.1.1
What does the phrase "pressurized container" mean? Explain using the concepts from previous lessons (e.g., particles, volume, number of particles). (min. 2 sentences)
Question 6.1.2
Why are we advised to protect it from sunlight and not expose it to temperatures higher than 50 degrees Celsius (≈122 degrees Fahrenheit)? What would happen if we did so? (min 3 sentences)
Note: Try to explain in narrative form (e.g., first ... would happen, then eventually ... happen because, finally .... happen because ...).
Also note: Try to include both micro-level events and macro-level events.
Question 6.1.3

Question 6.1.4
Do you think your understanding of objects like air duster cans, spray bottles, and balloons change after this unit? If yes, briefly explain how? (min. 2 sentences)
6.2. Putting the pieces together: developing an ideal gas equation
What we did in this unit was to re-develop three main gas theories using computational models and quantitative data analysis.
We defined the relationship between number of particles and pressure as:
- Qualitatively: As number of particles increases, pressure increases linearly (given that temperature and container volume are constant)
- Quantitatively: \((P)ressure = m_1 \times (N)umber \) , where \(m_1\) is a constant coefficient.
We defined the relationship between gas temperature and pressure as:
- Qualitatively: As gas temperature increases, pressure increases linearly (given that number of particles and container volume are constant)
- Quantitatively: \(P= m_2 \times (T)emperature \) , where \(m_2\) is a constant coefficient.
And, we defined the relationship between container volume and pressure as:
- Qualitatively: As gas temperature increases, pressure increases linearly (given that number of particles and container volume are constant)
- Quantitatively: \({P} = {m_3 \over (V)olume}\) , where \(m_3\) is a constant coefficient.
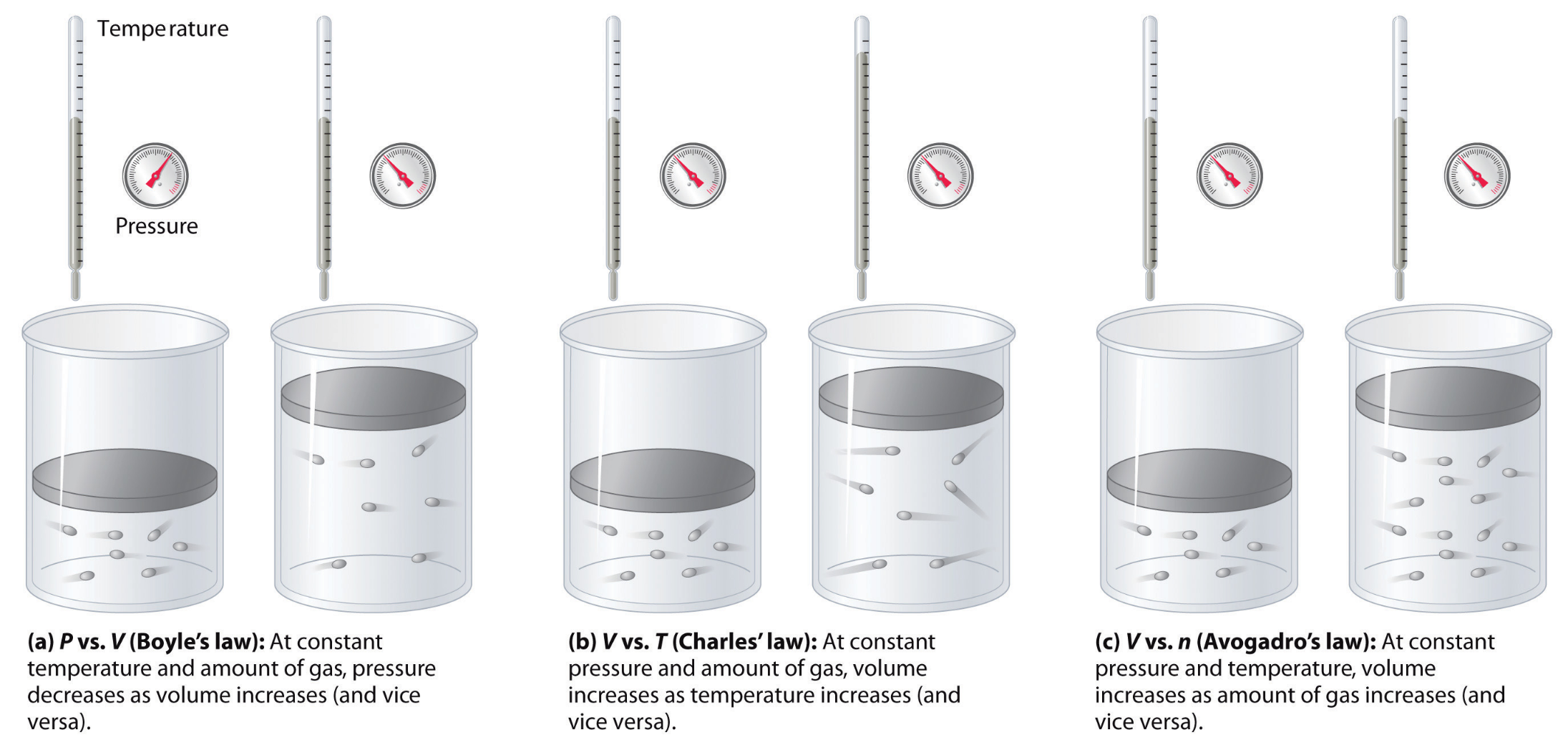
Our methodology and findings were analogous to three scientific discoveries made between 17th and 19th centuries:
However, as both the warning on the air duster can and the ballon-on-fire experiment showed, often times, we may not be able to explain gas-pressure related phenomena through just one variable. We need be combine our three theories and come up with one ideal gas theory. Let's try to do that!
Question 6.2.1
Can we put together our three findings in one coherent theory? Let's go ahead and give it a try!
First, write your combined theory verbally. Try to do it with just 1 coherent sentence.
Note: If you are having difficulty, you can write more than one sentence. It is perfectly fine.
Question 6.2.2
How about one mathematical equation that combines our three equations? Let's give it a try!
Alternative: If you are having difficulty in combining the equations, do not worry much. Either write the best equation you could come up with or write why you find this task particularly difficult.
6.3. Let's talk about our ideal gas theories
 Please set your computer aside briefly (do not close this page) and join the classroom discussion that your teacher is going to moderate.
Please set your computer aside briefly (do not close this page) and join the classroom discussion that your teacher is going to moderate.
Note: If your teacher did not initiate the discussion yet, you can start answering the first four questions below as you are waiting.
Question 6.3.1
If the discussion has not started yet, start answering the following question: Why even bother developing an ideal gas theory? In which situations such a mathematical theory might help us? (min 2. examples)
Question 6.3.2
Before moving on, please reflect on the classroom discussion briefly: (1) How did your verbal and mathematical ideal gas theory compared to the other groups' theories? (2) What were the similarities? (3) What were the differences? (min 2. sentences)
6.4. The ideal gas law: making the theory work
Let's review how we would put together our three theories mathematically:

\(P = m_1 \times N\) (Eq. 1)
\(P = m_2 \times T\) (Eq. 2)
\(P = {m_3 \over V}\) (Eq. 3)

\(P = {{(m_1 \times N) \times (m_2 \times T) \times (m_3)} \over V}\) (Eq. 4)
Step 3: We would slightly modify the equation by moving \(V\) to the other side of the equation and we would also get rid of the parentheses:
\(P \times V = {m_1 \times m_2 \times m_3 \times N \times T }\) (Eq. 5)
Finally, we would combine all three coefficients \((m_1 \times m_2 \times m_3)\)as one coefficient, which we can simply call as \(m_g\) or the ideal gas coefficient:
\(P \times V = {m_g \times N \times T }\) (Eq. 6)
Question 6.4.1
In the field of chemistry, our model is expressed slightly differently as \(P \times V = n \times R \times T\), where
- \(n\) corresponds to \(N\) or "number of particles" in our model, expressed in moles
- \(R\) corresponds to \(m\) or "gas coefficient" in our model, which is called the "universal gas constant."
- Its value is 0.08 L atm / mol K.
Answer the following chemistry problem using the ideal gas equation:
5 moles of nitrogen gas is in a 100 liter fixed cylinder at 300 Kelvin. What is the pressure of the gas?
Note: please determine the values of each of your independent variables (e.g., volume, temperature) and fill the data table below.
Question 6.4.2
Also answer the textbook question below:
Note: The temperature of air inside our lungs is approximately 37o C (273 + 37 = 310o K)
Question 6.4.3
Please describe how you solved the question above. Explain in steps. (min. 3 steps).
Such as:
- First, we did ....
- Then we did ....
- ....
Question 6.4.4
Optional question if you finished early: Answer the (b) part of the textbook question below. Also explain how you solved this problem.