What is the parameter of interest? What symbol is used to represent this value?
Overview
The purpose of this lesson is to give students hands-on experience with creating and using sampling distributions. Once the concept is understood, the lesson asks them to use sampling distributions to evaluate a claim (based on informal reasoning, we don’t introduce p-value yet). The sampling distributions will be generated using a NetLogo model. After using the model as it was created, students are asked to modify the NetLogo model to generate a modified sampling distribution.
Standards
Computational Thinking in STEM 2.0
- Computational Data Practices
- [CT-DATA-1] Using computation to collect and create data
- [CT-DATA-6] Using computation to analyze data
- Computational Modeling and Simulation Practices
- [CT-MODEL-1] Using computational models to understand a complex phenomenon
- [CT-MODEL-2] Using computational models to hypothesize and test predictions
Activities
- 1. Statistic vs. Parameter
- 2. Sampling by hand
- 3. What is a Sampling Distribution?
- 4. Sampling Distributions on a larger scale
- 5. Using a Sampling Distribution to reason about data
- 6. Final Thoughts
Student Directions and Resources
SWBAT (students will be able to): Define/recognize/use/describe the following:
- Parameter vs. Statistic
- Sampling Distribution
- Distribution of a Sample
- Distribution of a Population
SWBAT Evaluate claims using sampling distributions
1. Statistic vs. Parameter
A statistic is a number that describes some characteristic of a sample.
A parameter is a number that describes some characteristic of a population.
The table below shows three commonly used statistics and their corresponding parameters. These symbols are widely used in statistics and you are expected to know and use these symbols and terms. The symbol for sample mean is read "x bar" and the symbol for sample proportion is read "p hat." PLEASE get out your notebook and write down the following symbols and their meanings:
| Sample Statistic | Population Parameter | |
| \(\bar x\) (sample mean) | estimates | \(\mu\) (population mean) |
| \(\hat p\) (sample proportion) | estimates | \(p\) (population proportion) |
| sx (sample st. dev) | estimates | \(\sigma\) (population st. dev) |
Use the following scenario for the questions below:
From a large group of people who signed a card saying they intended to quit vaping, 1000 people were selected at random. It turned out that 210 (21%) of these individuals had not vaped over the past 6 months.
Question 1.1
Question 1.2
What is the statistic obtained from the sample? What symbol is used to represent this value?
2. Sampling by hand
Since we do a lot of small group work in AP Statistics, we’ve decided to sample 2 students from a group of 4 and take the average of their scores to get an estimate for how well students in this group performed on the exam. **Note: usually people wouldn’t use a sample and population this small, but we’re starting small to help you visualize what we’re doing.**
For this scenario, our population will be 4 students with the following scores: Alexis - 3, Bert - 4, Chris - 5, Devin - 5
Question 2.1
How many samples of size 2 can be taken from this population?
Question 2.2
What is the parameter of interest for this situation?
Question 2.3
What statistic are we using to estimate the parameter of interest for this situation?
Question 2.4
Do you think taking a sample this size from this population effectively estimates the mean score of the population?
3. What is a Sampling Distribution?
Since we do a lot of small group work in AP Statistics, we’ve decided to sample 2 students from a group of 4 and take the average of their scores to get an estimate for how well students in this group performed on the exam.
For this scenario, our population will be 4 students with the following scores: 3,4,5,5
Use the NetLogo model below to simulate choosing two students (n=2) at a time from this population (N=4).
1) Click "setup" to start the model. If you are bothered by a person being cutoff on the edge of the screen, click "setup" again.
2) Click "collect sample" to choose your first sample, and record your results in the table below before pressing the button again.
3) Continue pressing "collect sample" and entering data into the table below until all possible samples have been chosen.
*Note: you may have to add additional rows to the data table.
Question 3.1
Calculate the sample mean for all possible samples of size 2 from this population.
Question 3.2
Create a dotplot of your results from question #2. Create your sketch below.
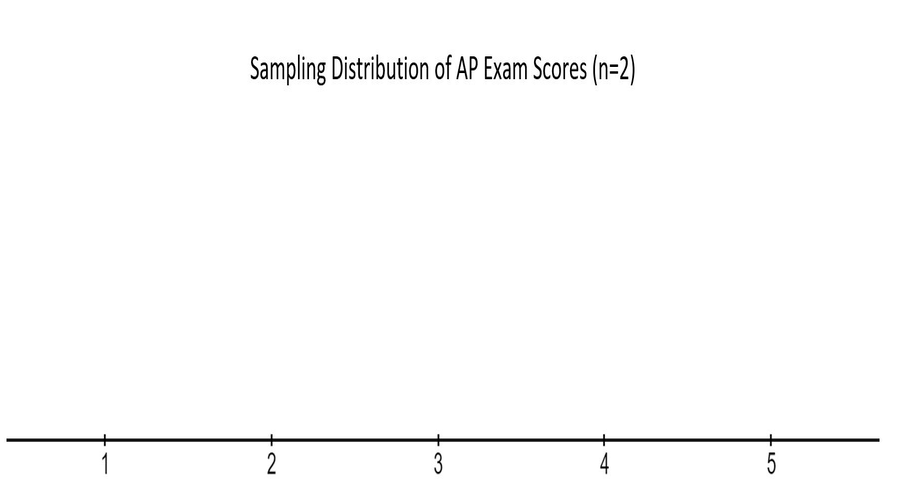
Question 3.3
In most real-life situations, we cannot create the dotplot of all possible samples of size n from the entire population (size N). Why not?
4. Sampling Distributions on a larger scale
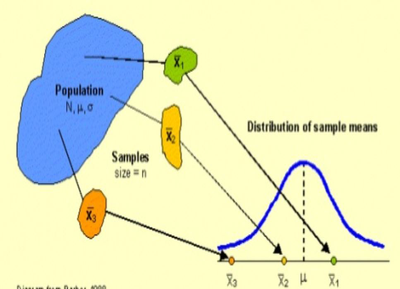
What you created on the previous page was the sampling distribution of AP scores for that group of 4 students. You took all six possible samples (n=2) from a population of four students (N=4). Sampling distributions are an important concept in Statistics and understanding what they are is the key to everything we do for the rest of the year.
A sampling distribution shows all possible samples of size n taken from a population of size N. In real-life scenarios, we don't create the entire sampling distribution by hand, or even using a computer, because our population is much larger (or it's size is unknown). For illustrative purposes we will use a NetLogo model to simulate taking samples of AP Statistics exam scores from last year. There were 48 students in our classes last year, and we’ll take samples of 2 students at a time.
Here's the new scenario:
Question 4.1
Click "setup" and then "collect sample". What did the model do?
Question 4.2
Press the "collect sample" button 30 times. Drag the word "Mean" from the table to the horizontal axis of the empty graph. The graph is starting to take shape, but it cannot be called a sampling distribution yet... Why not?
Question 4.3
A school administrator took a sample of 2 AP statistics students and found their average AP test score to be 1.5. Based on that sample, the Administrator is claiming that the mean test score for all AP stats students at ETHS is 1.5. Do you have substantial evidence to refute their claim? You just created a statistical model - use it to explain to the administrator that their estimate is probably wrong.
Question 4.4
What was wrong with the administrator's sample?
5. Using a Sampling Distribution to reason about data
We ran the model from the previous page until we collected every possible sample of 2 students. Below you can see the ENTIRE sampling distribution for our situation (n = 2, N = 48 students).
Question 5.1
On the left side of the screen you see a table. Click on one of the cells in the row with "index" 17. This should highlight one single dot on the dotplot. Explain what that dot represents in the context of the situation.
Question 5.2
Suppose an administrator is claiming that the true Mean score of the population is 3.2. Do you have convincing evidence to refute their claim? Explain.
6. Final Thoughts
Question 6.1
What is at least one big idea that you learned about sampling distributions in this lesson? Explain.
Question 6.2
Pick any computational tool/activity that you have used in this lesson. Briefly describe the tool and explain how you used it to learn.
Question 6.3
Indicate how much you agree or disagree with the following statement:
I enjoyed learning with the computational tools/activities in this lesson.
Disagree
In the middle / I don't know
Agree
Strongly agree
Question 6.4
Indicate how much you agree or disagree with the following statement:
I found this lesson more engaging compared to my other lessons without computational tools/activities,
Disagree
In the middle / I don't know
Agree
Strongly agree
Question 6.5
Indicate how much you agree or disagree with the following statement:
Compared to lessons without computational tools/activities, I found this lesson more challenging.
Disagree
In the middle / I don't know
Agree
Strongly agree
Question 6.6
Indicate how much you agree or disagree with the following statement:
I feel that I successfully learned the content of this lesson.
Disagree
In the middle / I don't know
Agree
Strongly agree
Question 6.7
Indicate how much you agree or disagree with the following statement:
I felt stressed by the computational tools/activities we have done in this lesson.
Disagree
In the middle / I don't know
Agree
Strongly agree
Question 6.8
Is anything that you learned in this lesson relevant to your personal aspirations? If yes, please explain.
