Lesson 2. Bias and Variability

Jacob Mills
Mathematics
1-40 minute class period
High School AP Statistics
v4

Overview

Students modify their sampling distribution model to see how the sampling distributions of biased and non-biased estimators compare and to investigate the effects of sample size on variability in a sampling distribution. Extra emphasis is given to the difference between bias and variability.

 

Standards

Computational Thinking in STEM 2.0
  • Computational Data Practices
  • Computational Modeling and Simulation Practices
    • [CT-MODEL-1] Using computational models to understand a complex phenomenon
    • [CT-MODEL-2] Using computational models to hypothesize and test predictions

Activities

  • 1. Intro to a new sampling model
  • 2. Biased Vs. Non-Biased Estimators
  • 3. Bias
  • 4. Sample size and variability
  • 5. Bias vs. Variability
  • 6. Reflection

Student Directions and Resources


SWBAT:

Understand/use/define Bias vs. Variability

Understand/use/define the relationship between sample size and variability

 

1. Intro to a new sampling model


In the previous lesson we learned about Sampling Distributions. We specifically looked at a sampling distribution of MEANS. In this lesson we're going to use the same model that we used in the previous lesson to create and compare sampling distributions for a few different statistics. (note all sampling distributions created in this lesson are actually approximations, they are not complete, but they are perfectly good for our purposes)

Scroll down to see instructions and questions for this page.

 


Question 1.1

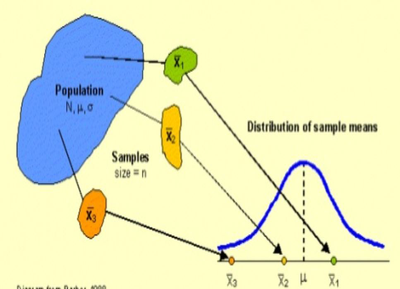
First, we'll create the same sampling distribution that we created yesterday. Use the model above to create the sampling distribution for the mean scores of samples of 2 students (n=2) taken from a population of 48 students (N=48).

1) Set the slider and click "setup" and "collect samples." The sampling will happen faster if you pull the "model speed" slider all the way to the right.

2) Click the button that says "tables" in the upper left, then "data set" in order to see your data table. You can drag it around in the CODAP window to wherever you want it.

3) Now we'll set up the graph. First, click the "graph" button in the top left. Then click the "click here" along the x-axis and select "mean."

4) We're also going to find the mean of the data in this graph (That is, the mean of all the means from each sample). To do that click on the ruler to the right of the graph and check "mean." There should now be a line in the middle of your sampling distribution for the mean, and you can hover over it to find out its value.

The mean score for our population of 48 students is 3.4. Is your mean close to that value?

2. Biased Vs. Non-Biased Estimators


Now we're going to do the same thing, except instead of calculating the mean score for our sample, we're going to calculate the MAXIMUM score of our sample. We (Mr. Mickelson and Mr. Mills) made this model, so we can change it in order to explore a different statistic. We're going to change the model to find the maximum of each sample. 

Note: If you need to start fresh just reload the page and everything will reset.

a) Underneath the model window is a tab called "netLogo Code". Click on that to open the code. Don't freak out, we're just going to make one little change!

b) Scroll down to find line 29. You can see the line numbers on the left side of the workspace. 

c) In lines 30 and 31 you should see the word "Mean." In both places, change the word Mean to the word Max.

d) Press recompile code at the top of the workspace.

e) Click setup and collect samples. This time the model will take the maximum value from each sample.

e) Click "tables," the "data set" again. Click "graph" and this time put the "Max" on the axis of the graph.

f) Add the mean to your graph of sample maximums (click the ruler, then check "Mean").

 


Question 2.1

For our population, what is the actual maximum? Is the mean of this sampling distribution close to that value?



Question 2.2

Now erase that data (either with the trashcan icon under "tables" or refreshing the page) and do the same thing using the minimum statistic (just repeat what you did for Max, just use the word Min).

Is the mean of this sampling distribution the same as the actual value of the population minimum?

3. Bias


On the previous pages you probably noticed that the center of the "Mean" sampling distribution lined up pretty closely with the center of the actual population distribution. However, the center of the "Max" and "Min" sampling distribution did not match up with the actual maximum and minimum of the population. The statistics "Max" and "Min" are examples of BIASED estimators. The mean of their sampling distribution is not equal to the actual value of the population parameter. 


Question 3.1

Do you think the mean is a biased estimator? Explain your reasoning.



Question 3.2

On the next page we'll use the same model but increase the size of our sample (n). What do you think will happen to the sampling distribution? How will that show up in the model?



Question 3.3

On the next page you'll be asked to use the model to see how sample size affects the variability of the sampling distribution.

Make a plan for how you'll use the model to investigate this question.

4. Sample size and variability


Here's the same model, but now we're back to calculating means. Scroll down for instructions!


Question 4.1

Use your plan and investigate how changing the sample size affects the variability of the sampling distribution (you can show the standard deviation on your graphs in the same way that we showed the mean, go back to page 1 if you need to!). Was your prediction on the previous page correct?



Question 4.2

By what factor do you need to increase the sample size in order for the standard deviation to be cut in half?



Question 4.3

By what factor do you think you need to increase sample size in order to reduce the standard deviation to 1/3 of it's value? 



Question 4.4

Based on you answers to the previous questions, make a guess about the formula for the standard deviation of a sampling distribution. In other words, what effect does sample size have on standard deviation and how does this show up in the formula? Use your knowledge from previous math courses to answer this question!



Question 4.5

When we're taking samples in real life in order to estimate the true value of a parameter, is it better to have more or less variation?

5. Bias vs. Variability


This is just a page to put together your understanding of bias and variability. A lot of times students say "more biased" when they really mean "less variable", so this is a pretty important thing to nail down!


Question 5.1

On pages 2-3 you learned about bias. On page 4 you learned about variability. Explain the difference between bias and variability in a way that a freshman could understand. You are welcome to use your book and the internet for more definitions and illustrations (I think your book has a really useful graphic on page 481).



Question 5.2

Ideally, we want the variation in our sampling distribution to be as _______ as possible.

  High
  Medium
  Low


Question 5.3

Two graduate students are studying the effects of a new cancer drug. Student A took a sample of size 10 from the population, while student B took a sample of size 30. Whose results will be more precise? Why? What do we mean by 'precise'?

6. Reflection


(Use the figure below for questions 1 and 2) 

The figure shows approximate sampling distributions of 4 different statistics intended to estimate the same parameter.


Question 6.1

Which statistics are unbiased estimators? Justify your answer.



Question 6.2

Which statistic does the best job of estimating the parameter? Explain your answer.



Question 6.3

The Evanstonian is collecting responses for an opinion poll. The editor suggests that they increase their sample size. The statistical reason for increasing the sample size of the opinion poll is to reduce _____________________________.

  bias of the estimates made from the data collected in the poll.
  variability of the estimates made from the data collected in the poll.
  effect of nonresponse on the poll.
  variability of opinions in the sample.
  variability of opinions in the population.