Students will develop an understanding of how populations interact with each  other within a community, discussing ideas concerning carrying capacity, competition, and interdependence. From there students will use models to explain the connection between genetic drift, natural selection, and speciation.

Think back to the activity in Lesson 1 where you modeled a simple ecosystem consisting of predators (wolves) and prey (moose).  As you may have observed during that activity, predator and prey populations oscillate  over time.  A graph of population data from Isle Royale is shown below as an example of these oscillations.  Two scientists (Lotka and Volterra) modeled these oscillations using differential equations.  A graph of these equations is provided for comparison.

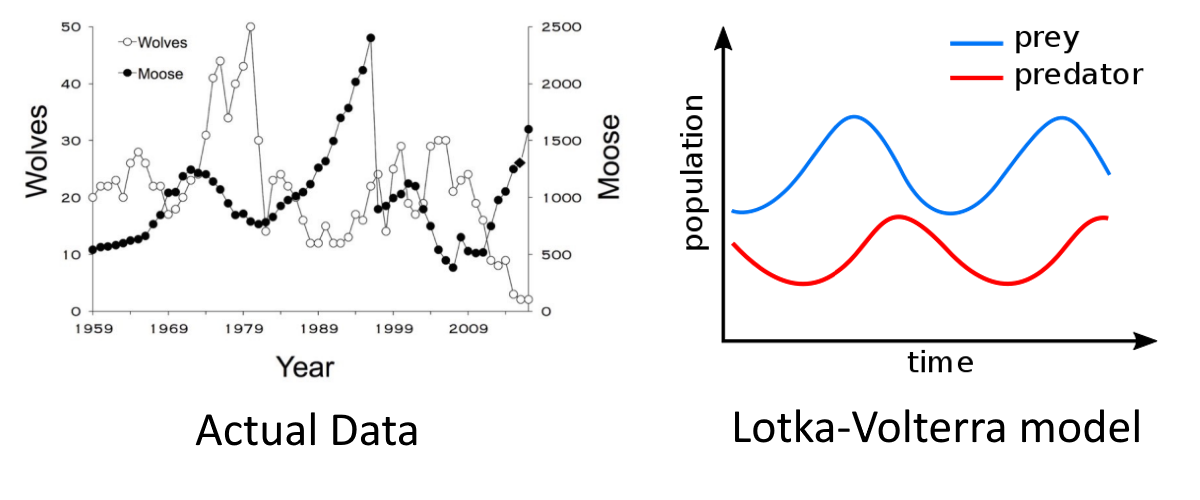
The equations used in this model state that these population oscillations are based on the birth and death rates of the predators and prey.  The model also claims that the prey death rate and the predator birth rate are proportional to the number of prey caught by the predators.

It is often helpful to understand how a model works before using it to investigate a phenomenon.  In this activity, you will look at and interpret some of the underlying code that governs how the model runs.  If you want to investigate beyond the questions in this activity, you can look at the complete code of any NetLogo model by clicking on the tab labeled 'NetLogo Code'.

All of the models you will see throughout this unit will have some things in common.  For example, every model has individuals called agents which interact with each other in a variety of ways based on rules that govern their behaviors.  Also, in every model, time moves forward in short steps called ticks.  At the end of each tick, the model uses the agents' rules to calculate what the state of the model will be in the next tick.  This means that to understand how the model works, it will be important to understand how the agents behave.

This model has two main types of agents, which are wolves and moose.  The questions below will address how each of them behaves. 

There are two main variations to this model that you will be working with.

In the first variation, wolves and moose wander randomly around the landscape, while the wolves look for moose to prey on. Each step costs the wolves energy, and they must eat moose in order to renew their energy. If wolves are unable to catch enough moose , they will die. At each time interval both wolves and moose have a fixed probability of reproducing, depending on the corresponding sliders.  This form of the model follows the same assumptions as the Lotka-Volterra equation-based model described earlier.

Basics of the model

1. Make sure to select the "moose-wolves" option in the model version dropdown menu.

2. Click the SETUP button.  You can click this button at any time to reset the simulation to its initial settings.

3. Press the GO button to begin the simulation.  If you press the GO button while the model is running, this will pause the simulation.

4. Look at the monitors to see the current population sizes.

5. On the top of the world view you will see the word “ticks” with a number next to it. Each tick represents a unit of time passing by.

6. Look at the POPULATIONS plot to watch the populations fluctuate over time.

The behaviors of these organisms are influenced by changing the values of the green sliders. Go ahead and mess around with the model and sliders to get used to interacting with it.

Before answering the questions, let the simulation run for at least 300 ticks and observe the interactions of the wolf and moose over that time.

As stated earlier, a stable system will tend to have a relatively steady population over the course of time, and an unstable system will eventually result in the extinction of one or more of the populations.

Your challenge at this point is to turn the "moose-wolves" ecosystem (which is based on the Lotka-Volterra equation-based model) into a stable system that allows for continuous generations of both wolves and moose for at least 300 ticks.

The variable "moose-wolves" must be selected in the model version dropdown menu.

You should only spend about 5-10 minutes on this activity.  Don't worry if you aren't able to find a way to stabilize the system.  Whether you stabilize it or not, describe your thought process by answering the questions below.

In the previous activity, you probably weren't able to find a way to stabilize the ecosystem for 300 ticks.  That is perfectly fine!  In fact, it is not possible to make that ecosystem stable over long periods of time.  In order to do that, there need to be some changes to the model itself, which you will explore next.

The second variation includes plants in addition to wolves and moose. The behavior of the wolves is identical to the first variation, however this time the moose must also eat plants in order to maintain their energy, and if they don’t they will die. Plants that are eaten by moose will regrow after a fixed amount of time depending on the plant regrowth time slider.

Select "moose-wolves-plant" in the model version dropdown menu. Keep all other settings the same.

Hit "setup" and "go" to start the simulation. Let the simulation run for 300 ticks before pausing the simulation by hitting "go" again and answering the questions.

Find three different ways that you can manipulate the simulation so that both populations die off without changing the initial population of either wolves or moose. When you figure this out, describe the variable(s) that you changed for each situation, and then explain why you think both populations were not able to survive.

Make sure to select "moose-wolves-plant" in the model version dropdown menu.

At the beginning of the lesson, you were introduced to an equation-based model of population dynamics.  In that model, population oscillations are based on the birth and death rates of the predators and prey, and the prey death rate and the predator birth rate are proportional to the number of prey caught by the predators.

Here you will evaluate and compare this equation-based model and the NetLogo model.